扫雷其实是一门学识 教你怎样快速提高扫雷技巧

  在简略的雷区中小试牛刀后，带着发现的规矩，让咱们进行一次实战演习。下图是高档扫雷游戏中的一个典型的雷区：

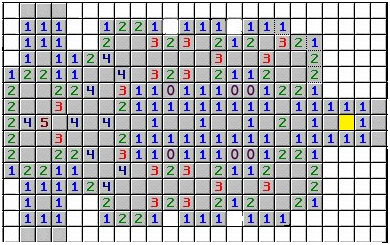
  你能在不翻开格子的情况下，直接指出黄格子中有无地雷吗？ 假如将雷区随意改动一点——左上角的一个格子下移一位，成果又怎样呢？

  你或许需求考量大局，从某个点开端慢慢地推理，将雷区悉数扫描一遍，才干判别。而当雷区恣意改动一点时，你都要从头来过，才干再次回答。这无疑是一种巨大本钱担负。

  实际上咱们我们能够很快速地给出答案：第一个雷区的黄格子中无雷。而第二个雷区的黄格子中一定有雷。

  这是怎样做到的？其实将上述的逻辑门引进到这个杂乱的雷区中，全部都会变得简略而明晰起来。

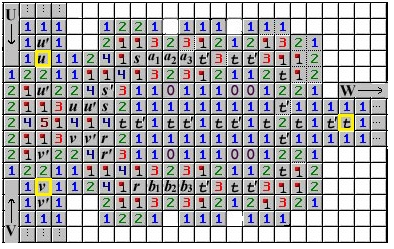
  雷区内接近鸿沟、能够直接确定是地雷的方位都插上了标明旗，剩余的方位标上了不同的字母。把一个有地雷格子看作1，没有地雷的看作0。最左面的格子（u、v）作为输入，最右面的格子（t）作为输出。依照扫雷游戏的规矩，通过一步步核算，它们之间的联系便是：

  明显，这个雷区被概括成了一个AND门，它不只轻松化解了这个扫雷难题，并且把雷区的规矩提醒出来了。如此一来，当你把握扫雷中这些逻辑门规矩并加以操练后，就能到达准确、快速的“机械化”扫雷水准。而到那时，一个新纪录或许就会诞生了。

  将扫雷问题抽象化然后缩短游戏时刻的人，也不单单是扫雷发烧玩家。一些数学家也非常重视这样的游戏背面的数学含义。

  英国一位数学家用扫雷游戏中的逻辑规矩构建了一系列电子元件，用电子电路模仿雷区。他企图将一个的给定的雷区图画交由核算机来判别是否可解。假如跟着格子数量的添加，电脑的核算量添加不是很快，便是P问题，假如核算量添加的很快，便是NP问题。核算机判别雷区是否可解，需求这类问题归于P问题才能够。

  关于几种根本的电路元件（AND、OR、NOT），假如将很多个这样的元件组合起来，相互连接，就会发生很多个输入、输出口。判别最终哪些输出成果能发生，哪些不能够发生的这类问题，被称为SAT问题，它归于一个经典的NP完全问题。

  而英国数学家的这样的一个问题在一些时分等同于一个杂乱电子电路的SAT问题，也便是NP完全问题。由此看来，面临一个上千上万个格子的巨型雷区，不要说去完结一切扫雷使命，就只是判别它是不是可解的，都或许会是核算机也承受不了的的大难题。